Introduction to Quantum Computing

Quantum computing is an emerging field with the potential to break many cryptographic algorithms. This is why it is especially important to understand what it is and how it works.

Concepts

The math behind quantum computing can be incredibly difficult and the principles are counterintuitive, as is always the case in quantum physics. This article aims to explain the concepts as simply as possible.

Spin

Every electron has an important property for quantum computing, called spin. Despite the name, spin is not directly what you expect It doesn’t mean the electron is literally spinning. As always in quantum physics it’s an abstraction of what it is. It is a characteristic of an electron.

It is possible to measure that spin of an electron, the spin can only be measured in two discrete states. This measurement always is done on a specified axis. The result of the measurement will be spin-up or spin-down.

If a qubit is measured the the qubit collapses to a definite state and it will behave like a classical bit afterwards.

Generally you can conclude this: You can prepare an electron so that it will have a specific spin when measured, but the act of measuring changes its state. In quantum mechanics, measurement always affects the system.

Qubit

A qubit is the basic unit of information in quantum computing. A qubit can be encoded by the spin of a electron or a photon. Qubits can also be encoded physically in many other ways, for example, using trapped ions or superconducting circuits.

Superposition

This is another principle of quantum computing and physics, a quantum state can be a linear combination of two basis states $\vert \uparrow\rangle$ and $\vert \downarrow\rangle$. In quantum computing these two states are usually $\vert 0 \rangle $ and $\vert 1 \rangle $. This linear combination in physics math is usually represented in the Dirac notation:

\[|\psi\rangle = \alpha | \uparrow \rangle + \beta | \downarrow \rangle\]

Here $\uparrow \rangle$ is the state of the particle in the spin-up position and $\downarrow$ is the spin-down position. For quantum computing, the two basis states are usually denoted as $\vert 0 \rangle $ and $\vert 1 \rangle $. Which means the equation is:

\[|\psi\rangle = \alpha | 0 \rangle + \beta | 1 \rangle\]

Both $\alpha$ and $\beta$ are complex numbers that satisfy the normalization condition:

\[|\alpha|^2 + |\beta|^2 = 1\]

Superposition in combination with entanglement and interference means that you can encode complex problems in such a state. A qubit can hold more information than a classical bit.

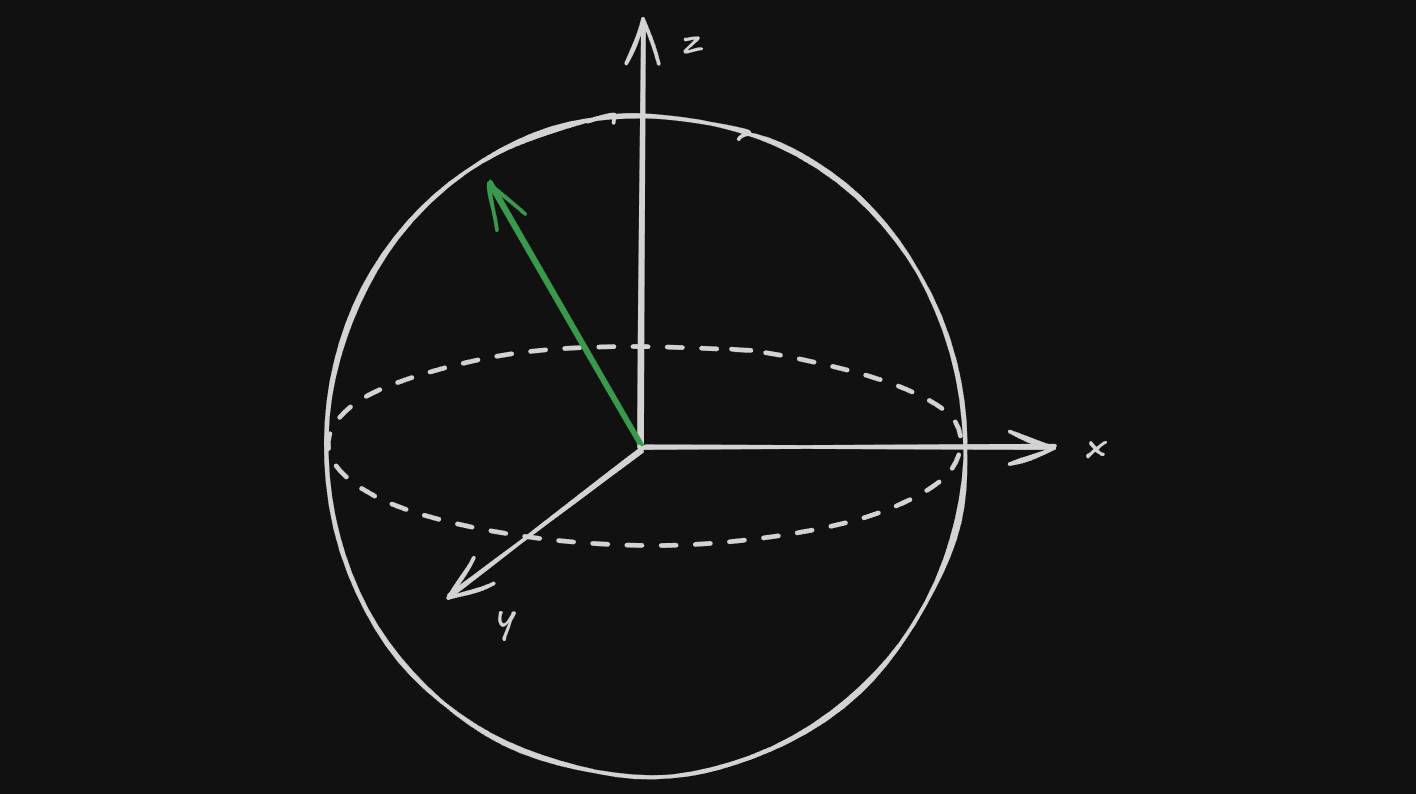
A qubit can be represented using a Bloch sphere where the green vector is the linear combination of the two basis states.

Entanglement

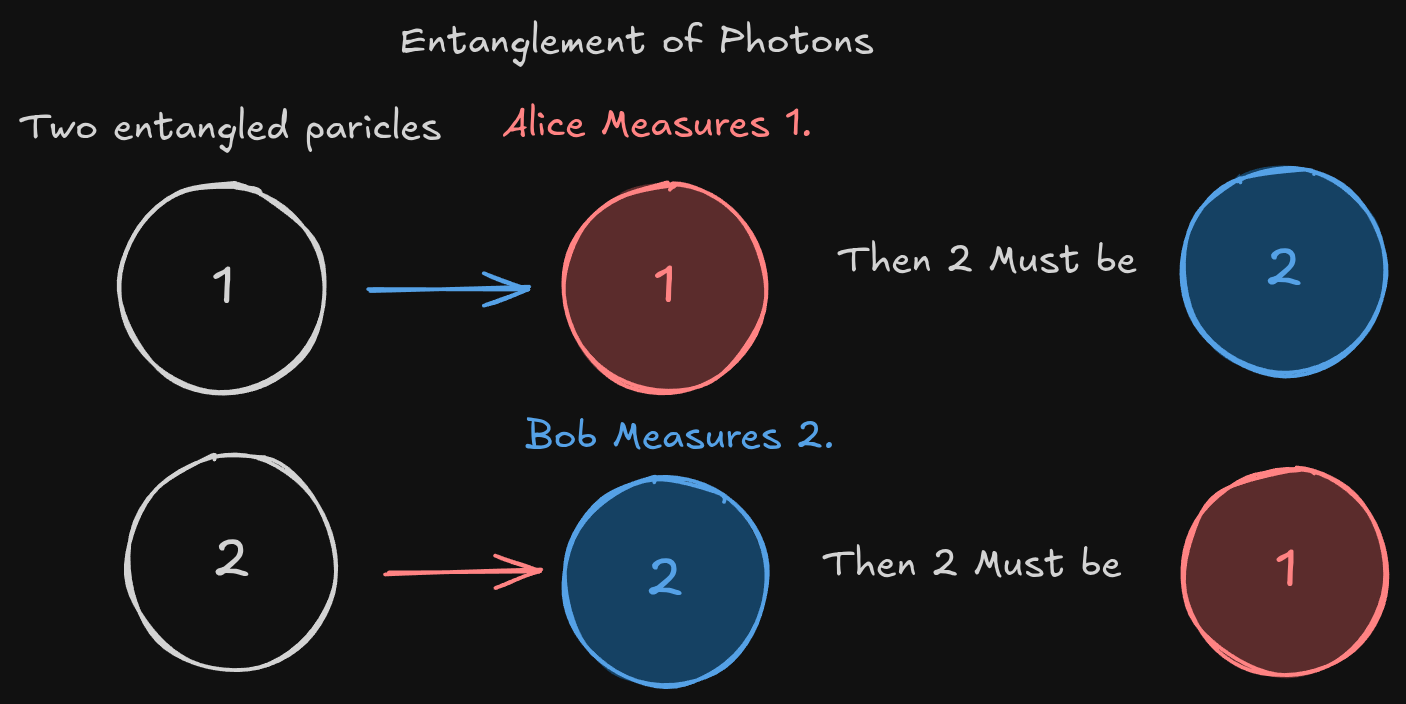
Two qubits can be entangled. In this state you cannot describe the quantum state of the particle independently. If two entangled particles (for example electrons, photons or trapped ions) are separated by a large distance the measurement of one qubit immediately determines the outcome of the measurement of the second qubit. This phenomenon is known as quantum non-locality.

Even though the measurements of both particles are correlated, this doesn’t allow faster-than-light communication, the measurements are random.

In the example we use white as the unknown state after the particles are entangled. Red is one measured state (for example spin-up) and blue is the other measured state (for example spin-down). If one state is measured the state of the other entangled particle is immediately known.

Issues An issue for all these principles is that the environment must not affect the particle/qubit. If a qubit is affected by the environment the two correlated states are unentangled, known as decoherence. This is one of the many issues in quantum computing it is physically challenging to implement the theoretical ideas practically. Additionally you need to account for errors and must find and eliminate them.

Probability

In quantum mechanics you always work with probabilities. The outcomes of measurements are not deterministic, they are given by the probabilities.

The equations above in the section Superposition are needed for understanding the probability when performing the measurement.

If the apparatus is aligned with the bloch sphere of the qubit the probabilities are fairly simple to calculate:

\[P(0)= ∣\alpha∣^2\] \[P(1)=∣ \beta ∣^2\]

The probabilities are calculated by squaring the complex numbers $\alpha$ and $\beta$. Here is a short example:

\[P(0) = |\alpha|^2 = (0.6)^2 = 0.36\] \[P(1) = |\beta|^2 = (0.8)^2 = 0.64\]

So in this quantum state the probability of the measurement being a $0$ is 36% and the chance of being a $1$ is 64%. If it is not aligned the basis vectors of the up and down direction need to be rotated after doing that the probabilities can be calculated again.

Interference

Superposition leads to interference. Different states interfere with each other, which results in constructive and destructive interference. This can influence the outcome of measurements.

Technical

To minimize the susceptibility of qubits to the environment quantum computers are cooled to minimal temperatures using massive refrigeration systems. Obviously quantum computers look totally different to classical computers.

Gates

Quantum computers also contain gates like classical computers. Here are three basic gates used:

• A NOT gate, usually called X gate, this will invert $\vert 0 \rangle$ to $\vert 1 \rangle$ and $\vert 1 \rangle$ to $\vert 0 \rangle$
• A Hadamard Gate, this gate is one of the most important gates in quantum computing, this gate is often used to put standard basis vectors into the superposition state, although this depends on the input
• A CNOT gate, which flips the state of the second input if the first input is active. This gate is used for entanglement.

To fully understand quantum computing, you need the math behind it, but to keep it simple this isn’t included here, if you are interested check out this video on YouTube.

Achievements

Currently the major players in quantum computing are Google, Microsoft and IBM.

IBM’s Public Quantum Computer

In 2016 IBM released the IBM Quantum Experience, this allows you to use quantum computers through the cloud. With these quantum computers and this repository you can generate real random numbers.

Google’s Quantum Supremacy Claim

In 2019 Google researchers claimed they have solved a task using a quantum computer with 53 qubits, which would take a classical computer approximately 10,000 years to solve. IBM then showed that the problem can be solved in just 2.5 days by simplifying the problem.

Until this point these achievements made by both companies are small steps to a world of quantum computers but not world breaking.

Microsoft Released Majorana 1

In February 2025, Microsoft released Majorana 1 which is a new quantum chip which can fit up to 8 qubits. The chip uses a different approach to achieve less susceptibility to the environment, it uses topological quantum computing, this again becomes exponentially difficult when understanding it.

Summary

Quantum computing is a rapidly evolving topic which is definitely one of the most interesting ones in the current age of computers. It may be able to break large parts of the current state cryptography, which could cause massive damage. Although it is often in the news and feared because of the reasons mentioned, the understanding of it is not that widely spread. One barrier to understanding the topic is that it is not as intuitive as normal physics, and it can become very difficult due to its basis in quantum mechanics.

References

1. https://www.scientificamerican.com/video/how-does-a-quantum-computer-work/ (Very useful video for a basic understanding)
2. https://www.youtube.com/watch?v=ZuvK-od647c (Veritasium Entanglement & Bells Experiment)
3. https://www.youtube.com/watch?v=qJZ1Ez28C-A (Superposition)
4. https://eitca.org/quantum-information/eitc-qi-qif-quantum-information-fundamentals/introduction-to-quantum-information/qubits/examination-review-qubits/what-happens-to-a-qubit-when-it-is-measured/
5. https://www.youtube.com/watch?v=-UrdExQW0cs (Exposing Why Quantum Computers Are Already A Threat)
6. https://pubs.aip.org/physicstoday/online/4795/What-s-under-the-hood-of-a-quantum-computer
7. https://en.wikipedia.org/wiki/Majorana_1